Investigations
into the Doomsday Argument
- (c) Nick Bostrom
- Dept. of Philosophy, Logic and Scientific method
- London School of Economics; Houghton St.; WC2A AE; London; UK
Back to anthropic-principle.com
The Doomsday argument in a nutshell
The Doomsday argument was conceived by the astrophysicist
Brandon Carter some fifteen years ago, and it has since been developed in a Nature
article by Richard Gott [1993], and in several papers by philosopher John Leslie and
especially in his recent monograph The End of The World (Leslie [1996]). The core
idea is this. Imagine that two big urns are put in front of you, and you know that one of
them contains ten balls and the other a million, but you are ignorant as to which is
which. You know the balls in each urn are numbered 1, 2, 3, 4 ... etc. Now you take a ball
at random from the left urn, and it is number 7. Clearly, this is a strong indication that
that urn contains only ten balls. If originally the odds were fifty-fifty, a swift
application of Bayes' theorem gives you the posterior probability that the left urn is the
one with only ten balls. (Pposterior (L=10) = 0.999990). But now consider the case where
instead of the urns you have two possible human races, and instead of balls you have
individuals, ranked according to birth order. As a matter of fact, you happen to find that
your rank is about sixty billion. Now, say Carter and Leslie, we should reason in the same
way as we did with the urns. That you should have a rank of sixty billion or so is much
more likely if only 100 billion persons will ever have lived than if there will be many
trillion persons. Therefore, by Bayes' theorem, you should update your beliefs about
mankind's prospects and realise that an impending doomsday is much more probable than you
have hitherto thought.
Consider the objection: "But isn't the probability that I will have any
given rank always lower the more persons there will have been? I must be unusual in some
respects, and any particular rank number would be highly improbable; but surely
that cannot be used as an argument to show that there are probably only a few
persons?"
In order for a probability shift to occur, you have to conditionalise on evidence that
is more probable on one hypothesis than on the other. When you consider your rank in the
DA, the only fact about that number that is relevant is that it is lower than the total
number of individuals that would have existed in either hypothesis, while for all you
knew, it could have turned out to be a number higher than the total number of people that
would have lived on one of the hypothesis, thereby refuting that hypothesis. It makes no
difference whether you perform the calculation with a specific rank or an interval within
which the true rank lies. The Bayesian calculation turns out the same posterior
probability. The fact that you discover that you have this particular rank value gives you
information only because you didn't know that you wouldn't discover a rank value that
would have been incompatible with the hypothesis that there would have existed but few
individuals. It is presupposed that you knew what rank values were compatible with which
hypothesis. It is true that for any particular rank number, finding that you have
that rank number is an improbable event, but a probability shift occurs not because of its
improbability per se, but because of the difference between its conditional
probabilities relative to either of the two hypotheses.
There are numerous objections such as this one, objections that can easily be seen to
be mistaken. When people first encounter the Doomsday argument (hereafter the DA), what
happens is that most of them think that it is obviously false. Then any sign of consensus
disappears when it comes to explaining what is wrong with it. Each comes up with his own
objection, these objections tend to be incompatible with each other, and typically they
rest on simple misunderstandings. This paper will zoom in on those features of the DA that
are genuinely problematic.
A probability shift must be made
In the case of the two urns, or in any similar situation
when we take a random sample, we should obviously draw a conclusion analogous to the one
aimed at in the DA. This follows from indubitable Bayesian principles, and anyone denying
this is invited to demonstrate his sincerity by betting according to his doctrine in an
urn game with the author of this paper.
If we have agreed on that as a starting point then we can take the next step towards
establishing the necessity of a probability shift by considering the following thought
example (discussed in Leslie[1996]).
The amnesia chamber
Imagine you are in an isolation chamber and don't not know what
birth rank you have, but let the two exclusive hypotheses MANY (= many people will have
existed) and FEW (=few people will have existed) be equally probable relative to your
present information set. Suppose you obtain a new piece of evidence: your rank is higher
than the number of individuals in FEW. That conclusively proves that MANY is true. This
implies that if you had instead found that you had a rank that was low enough to be
compatible with both hypotheses, then that would have increased the probability of FEW;
because if you thought that the new piece of evidence could lower but never raise the
probability of FEW, then you would be inconsistent, as is easily shown by a standard Dutch
Book argument, or more simply by the following little calculation.
Write "M" for "MANY", and "¬M" for "FEW"; and
let e be the evidence that you are living "early", i.e. that you have a rank
compatible with FEW. We can assume that  . Then
we have
. Then
we have

and
 .
.
Dividing these two equations and using  , we
get
, we
get
 .
.
So the quotients between the probabilities of MANY and FEW is less after e is
known than before. In other words, learning e decreases the likelihood of MANY and
increases the likelihood of FEW. Therefore, in the amnesia chamber experiment, a
probability shift results from learning e.
The next step is to determine whether it is an illegitimate idealisation to assume, as
we did, that you just got to know what your rank is. In reality, of course, there was
never any doubt: you knew all along that you were living in the 1990s. But the crucial
consideration is not when you obtained the evidence, but whether you have taken it
fully into account. Presumably, when you pondered over the future of mankind before you
first heard of the DA, you didn't take the datum that you are alive in 1997 fully into
account, for you didn't then realise all its implications. Now, when an important new
implication (i.e. that this fact can be used to argue for the likelihood of an impending
extinction of mankind), has been pointed out to you, you should make up for your earlier
neglect by updating your beliefs accordingly. It therefore seems that nothing essential in
the thought experiment hinges on the assumption that you were until recently ignorant of
your birth rank.
And this seems to be enough to show that a shift must be made. There are, however, a
number of hidden assumptions that we have made, if we are thinking of the amnesia chamber
experiment as establishing the DA, and these have to be brought out into the light. We
will have to go over them carefully before we can assess the validity or otherwise of the
DA. The chief ones I will discuss in this paper concern
- The no-outsiders requirement
- The reference class problem
- The Self-Indication axiom
A whole lot of other objections have been raised as well, but I think they have been
satisfactorily answered by Leslie. Rather than repeating the replies here, I refer the
reader to Leslie's work.
The no-outsider requirement
Instead of skipping directly to my own view on the
no-outsider requirement, we will warm up by conducting another thought experiment, which
will also serve the didactic purpose of improving our intuitive grip on how DA-style
reasoning works.
The four-buildings experiment
"Imagine four tall buildings with 100 floors each. You are
in a group of 303 people to take part in an experiment. You are told the following: All
participants will be anaesthetised and randomly carried to windowless rooms (the
lavatories) in the four buildings. In three buildings there will be one subject on each
floor; in the forth, there will be one subject on each of the first three floors and the
rest of the house will be empty. Then a tetragon die will be thrown to randomly select one
building. All subjects in that building will be given a stimulant so that they wake up
from their dreamless slumber. They might be offered bets of various kinds, which have been
prepared by the experimenter in advance, before the die was thrown. Ready?
Consider first the case of an outside observer. She selects a house at random. If she
looks at the 50th floor and there is someone there, then that proves, of course, that that
building contains 100 persons. If there is nobody there, the building contains three
persons. If she instead looks at the 3rd floor, she will get no information, since she
already knows that in all houses there are persons there. Suppose now that she randomly
chooses a name, Mr. N.N., from the participants list, and that the position of Mr. N.N. is
then pointed out to her. If Mr. N.N. is somewhere between floor 4 and 100, then that house
contains 100 persons. But what if Mr. N.N. is on floor 2? Again that would give the
outsider no information: the odds that the building contains 100 persons would still be
3:1. In this case, the unlikelihood that Mr. N.N. would be on one of the first three
floors given that he is in a 100-persons building is precisely balanced by the greater
likelihood that Mr. N.N should be in such a building in the first place. (We shall come
back to this consideration in a later section.) The overwhelming majority, after all, are
in 100-persons buildings. Only if a building is selected, and a name is picked randomly from
a list of the persons in that building, can we use the fact that the name denotes a
person on the 2nd floor to infer that the probability that it is a 100-persons house is
less than 75%. (In fact, it's 8%.) If this were the relevant analogy, then the Doomsday
argument would be valid.
But now consider the case of an insider. You wake up in a lavatory and remember the
experimental set-up. You begin to consider what odds you would take if offered a bet on
whether you are in a 100-persons building. After a little reflection you decide the
probability is 300/303=99%, rather than 75%. Why? Because, on average, 99% of all awake
persons in experiments of this sort will find themselves in 100-person buildings, and you
have no other relevant information than that you are an awake person in such an
experiment. The very fact that you are awake indicates that it is a 100-person building
that has had its inhabitants woken.
If you think otherwise, we may repeat the experiment a thousand times, and if you are
willing to bet according to your estimations, and do not change your mind, you will lose
money. If the experiment is repeated only 5 times, there is some chance that you will be
lucky and win despite your mistaken estimation, and even more so if the experiment is
performed only once; but it would still be rational to bet against you. However, no bet is
offered.
After a while, the lavatory doors are unlocked and you enter a room where there is a
window. You look out and are surprised to discover that you are on the second floor. The
probability that you are in a 100-person building obviously decreases; the question is by
how much. If this is a situation where a calculation based on a naïve application of the
DA is applicable, then the new probability that you are in a 100-person building should be
8%. But that is a loser's odds. The real probability is 75%. There is a note on the wall
beside the window written by the experimenter (from Monte-Carlo, we may suppose). It says
that if you sign it, you will be given $100 if you are in a 100-person building and have
to pay $1000 if you aren't. Having been convinced by John Leslie’s book, you sign it.
The next day the experimenter performs the experiment with another group of subjects. On
average, he makes $8700 per four days of work.
If this is right then there is an essential difference between the outsider case and
the insider case. In the former, there is a 8% chance that the person in question is in a
100-persons building; in the latter, the probability is 75%. The difference is that in the
outsider case, the tendency for the sample person to be in a 100-persons building because
most persons are in such buildings is offset by the postulate that the sample will be
taken from inhabitants of a given house, and this house is selected without regard to how
many persons there are in it. In the insider case, on the other hand, the sample and the
building are selected independently. The coincidence that the building selected happens to
contain the independently selected sample (i.e. you) indicates that the building was one
with a large population of samples, i.e. many inhabitants. As we have seen, this
difference results in different rational odds, the "rational odds" being defined
as the best odds one could give without having a negative expected utility from a
corresponding bet. So on which of the two cases, if any, should we model our situation
when it comes to the prospect of Doomsday? Clearly we are insiders with respect to the
human species.
To make the parallels explicit: The four buildings can be thought of as possible
worlds, and the sleeping people as possible observers; the awakened observers are the real
humans that will have existed; your discovery that you are on the second floor is the
observation that relatively few humans have existed before you; the fact that non-dreaming
sleeping subjects can't really think or make observations corresponds to the same fact
about non-existing "possible" observers; the proportion between 100-person
buildings and 3-persons buildings (chosen to be 3:1 just as an illustration) represents
the prior probability we would assign to the proposition that mankind will not have become
extinct by 2150, based on our direct estimates of the dangers of warfare, plagues, runaway
global warming, high-energy experiments etc.; and so on."
Leslie seems to accept that the thought experiment describes a situation relevantly
analogous to our own, though with one proviso. The experiment must be carried out only
once. If the experiment were repeated a great number of times, the odds would
asymptotically approach the one I gave above. But if the experiment is performed only once
or a small number of times, then, according to Leslie, another principle applies and we
should no longer be guided by estimates of expected utility when we determine what the
probability for being in a 3-person building is.
This reply might sound extremely as hoc and bizarre, but in fact it isn't. To
explain how one could be led to make this reply if one accepts Leslie’s position, we
shall do a thought experiment. (I know it's an awful lot of thought experiments here, but
for some reason they are very helpful when we are dealing with the DA.)
God's coin tosses
Suppose you know that you were created as the result of a divine
coin toss; if the coin landed heads, ten humans were created; if tails, only one human was
created. We assume that there are no humans other than those created as a result of this
coin toss, and that the everybody kept in isolation so nobody can see anybody else. Now
you, dear reader, are luckily alive; the question is whether this gives you any reason to
believe that God’s coin landed heads, or whether you should rather believe that the
chance is fifty-fifty. According to Leslie, you should believe the latter.
Here we see the reason why Leslie insists that my thought experiment should be carried
out only once. If God had tossed His coin a great many times, and created either ten or
one human for each toss depending on how the coin landed, then Leslie would agree that you
should say that the probability that you were created as a result of a toss wherein
God’s coin landed heads approaches 10:1. For in this case, we could contrast the size
of the group of people created as a result of the heads outcome with that of the group of
those created on a tails outcome. And these would all be actual, living humans. In the
case where God’s coin is tossed only once, there would only be one group of humans.
(In order not to complicate things with the possibility that you could have been God, let
us assume that in this thought experiment "God" is a fanciful way of denoting an
automatic randomised human breeder machine.) The other group would consist of merely
"possible humans", and, of course, a merely possible human doesn’t actually
think or "find herself in this or that situation". So in this case you gain no
information from the fact that you find yourself alive that you could use to infer that
God’s coin has probably landed heads; for how could you possibly have found yourself
otherwise than alive?
Setting the latter claim (that finding yourself alive makes the larger group more
likely, when the coin is tossed only once) to a side for the moment, we can at least agree
that in the case when the coin is tossed many times, say a thousand times, it is
more likely to be in the larger group. For the probability of belonging to a group of
people is equal to the sum of the probabilities of being the particular individuals in
that group. This is an immediate consequence of Kolmogorov's additivity axiom, since the
alternatives are mutually exclusive: one cannot be more than one individual. Think of it
like this: You know there are almost certainly about 5000 people. Hence there are about
5000 names of people. You know one of these names is yours, but you have absolutely no
idea as to which one it is. By the principle of indifference, you should therefore believe
that the probability that your name is among the names of persons who were created as a
result of a heads toss is about 90%, for about ninety percent of all the names belong to
such persons.
(If you are uncomfortable with this appeal to the principle of indifference, we can
perhaps add further persuasion by considering a variant of the God's coin tosses
experiment, where, instead of humans being created, the coin tosses result only in that
either one or ten names of randomly chosen humans from an extant population get entered
into columns of special list, either as "one-names" or as "ten-names".
After a thousand tosses, you get to know that you are on the list and you are asked to
guess in which column your name appears. (No other information is available, and you know
that all people on the list are given the same instruction.) Here it would be easy to
carry out a betting session in a scaled-down realisation of this experiment. Anybody who
now thinks that the chances should be fifty-fifty is encouraged to contact the author in
private. But nothing essential differs here from the original God's coin tosses with a
thousand throws; the fact that it is your mode of creation in one case and the status of
your name in the other makes no difference in this idealized context.)
So in order for the four-buildings example to model our true situation, the experiment
has to be performed once only. (Forget about the possibility of extraterrestrials for the
moment.) That is Leslie's position. However, upon reflection I have come to believe that
not even when the experiment is only done once is the four-buildings model correct. For it
is clearly supposed to be carried out in the real world, here on Earth, where there are
about six billion outsiders; not in a possible world where the experimental subjects and
the experimenter were the only beings that existed. And as we shall now see, that makes a
crucial difference.
Consider a universe where there are a thousand humans. Then a coin is tossed and either
one or ten more humans are created as a result. Now suppose that you discovered that you
were in such a universe (after the coin was tossed). The most probable hypothesis is of
course that you weren't created because of the coin toss but are one of the thousand that
were there anyway. But it is still ten times more likely that you were created as a result
of a heads-toss than a tails-toss. For consider the conditional probability Pr(I was
created because of the coin toss. | There are 1010 humans.). This is clearly greater than
Pr(I was created because of the coin toss. | There are 1001 humans.) If there are 1010
humans then about 1% of them will be coin-toss humans; if there are 1001, then the figure
is about 0.1%. By Bayes' theorem, we conclude that after conditionalising on "I was
created as a result of the coin toss." it is more likely (by about a factor 10) that
the coin landed heads than that it landed tails. So in this case, where we have a thousand
outsiders, if I know that I was created as a result of a coin toss, then that gives me
strong reason to believe that that coin toss landed heads; in contrast to the case where
there were no outsiders and the coin was only tossed once, where knowing that I was
created as a result of the coin toss didn't modify the prior fifty-fifty probability
distribution.
Thus we see that what is relevant is not how many times the experiments are
repeated, but how many people are expected to exist independently of their outcome. Since
this point isn't made in Leslie's work, it's worth epitomizing it by giving it a
mathematical formulation:
The Generalized DA formula (GDA)
In the simplified case where mankind is the only intelligent
species ever to exist (i.e. there are no outsiders) and considering only the two
alternatives FEW and MANY, we can calculate the conditional probability Pr(h|e) of a
long-lasting human race upon finding oneself alive at an early time by means of Bayes'
theorem in the following form:

We have just seen that the DA in this form would be incorrect in case we couldn't be
sure that there were no extraterrestrials. What we now want to do is to develop a way of
calculating what predictions the DA would make in the more general case where there might
be extraterrestrials. In order to do that, we shall consider again the model of God's coin
tosses, but this time the coin can be tossed any given number of times and there can also
be a group of outsiders that exist independently of the coin tosses.
We'll begin by making some definitions. Let "the group" consist of all
individuals that are created as a result of the coin tosses, i.e. the insiders. Let
"the reservoir" consist of all the other individuals, i.e. the outsiders; and
let R be the number of these. Let G be the hypothesis that you are in the group. Let e be
the evidence that you find yourself early, i.e. that within the batch in which you
were created you have a rank that is compatible with that batch being one that contained
only few individuals, i.e. being one that was created as a result of the coin landing
tails. Let Hk be the hypothesis that the coin landed heads k times.
Then the probability that the coin (when all the tosses are completed) having landed
heads k times is

(Where N is the number of times the coin is tossed.) The number of people in the group,
given that k heads turned up, will then be

(Where m is the number of people that are created each time the coin lands heads, and f
the number each time it lands.) The probability that you will be in the group, given that
the coin landed heads k times is

From the general relationship

we get
 (#)
(#)
Likewise, we can write

since  . Using
. Using  and inserting into (#) and simplifying, we get
and inserting into (#) and simplifying, we get
 .
.
Rejecting the SIA (to be defined in a later section), at least for the sake of the
present argument, the prior probability of M (you being born as a result of a toss where
the coin landed heads) is expressed by the weighted sum over the possible fractions of all
people that were created as a result of such coin tosses in the different possible
scenarios:
 .
.
Now we can define a new probability distribution, P', where the priors have changed to
accommodate the added information that you are in the group (i.e. were created as a result
of a coin toss):
 (*)
(*)
But from Bayes' theorem applied to this new distribution it now follows that

where all terms are known:




Inserting these values finally gives us
 (GDA)
(GDA)
which we can call the generalised Doomsday argument formula, the GDA. It should
be straightforward, using standard probability theory, to extend this result to cover
other cases where instead of a coin toss we have a process with more than two possible
outcomes, each with a different probability, and so fourth. Thus we have given an exact
expression of what happens on the DA point of view in the general case where an unknown
number of aliens may exist.
The reference class problem
The DA is formulated in terms of the number of people
that would have existed in different scenarios, but "people" is a fussy concept:
there are in the early stages of our species a big grey zone where it is unclear what to
count as human and what as ape, and it is not implausible that in the future, if we manage
to survive, we will change into something else or perhaps replace ourselves with
computers, our "mind children" (Moravec [1989]). In itself the fussiness may not
be very harmful for the DA, but it raises the suspicion that it might be a symptom of some
more fundamental affliction. In any case, the fussiness is so extensive, especially in the
future direction, that unless we make more precise what we are supposed to include in the
reference class, the conclusion of the DA, even if it followed from its premises, would be
so vague as to be of strongly reduced practical import.
Part of Leslie's answer (Leslie [1996], pp. 256-63) to this problem is to point out
another feature of the analogy with the urn experiment that we used to introduce the DA in
this paper. If the balls in the urn, instead of being numbered, had been of different
colors and shades of colors, and we asked "What fraction of the balls in this urn is
red?", then we would have been faced with the problem of what nuances of pink and
purple to count as red. But here the answer would be that it would simply be up to us to
decide. If we are interested in how many light-red-to-dark-purple balls there are, then
what we should put into the Bayes’ formula is our estimate of the number of such
balls; and when we draw the first ball, all we have to do is classify it either as
light-red-to-dark-purple or as not-light-red-to-dark purple and then calculate the
posterior probability in the same way as in the case with numbered balls.
This solves a part of the problem. If we are interested in how many blue-eyed humans
there will exist, then we do the calculation with the parameters for blue-eyed humans; if
we ask about the number of two-or-three-eyed humanoid descendants, then our beliefs and
data about those are what should be fed to the equation. Bayes' formula is perfectly
neutral as to how to define the hypotheses.
This response can only be part of the answer, however. As Leslie realises, for the
purpose of the DA, it is necessary to place restrictions on which reference classes are
permissible; otherwise they could be both too wide and too narrow. Let's begin by showing
that they could be too wide.
Suppose we were interested in finding out how many oaks-or-humans there will have
existed on Earth. (Set to a side for the moment the difficulty of exactly what to count as
a human or a an oak tree.) Suppose we had reduced the quandary to two rival hypotheses:
either (h1) there will have been 100 billion humans and 100 billion oaks, or else (h2) 100
billion humans and 1000 oaks. Now you find yourself alive at a time when there so far have
been 50 billion humans and 50 billion oaks (say). In this case, it would obviously be
wrong to reason that h1 is now much more likely than h2 because we have discovered that a
random sample (you) turned out to be among the first 100 oaks-or-humans and that would be
much more likely on h1 than on h2. The reason why it would obviously be wrong to reason
thus is that you are clearly not a random sample from the population of oaks-or-humans:
you couldn't possibly in any meaningful sense have turned out to be an oak. (We are
assuming here that oaks don't have souls or such; which of course they haven't.)
This raises another question: "From what population am I a random sample for the
purposes of the DA?". In my opinion, this turns out to be the problem in
assessing the DA, and we will address it in a later section. For now, we can at least
conclude that the reference class must be restricted in some way: it can't be made as
inclusive as one pleases.
It can't be made arbitrarily restrictive either. For instance, we can't hope to derive
any valid conclusions if we define the reference class to consist of all humans born the
day you were born or later. Relative to that group you would indeed have had an
exceptionally low rank, but there is nothing surprising about that and nothing follows
from that fact about how long you should expect the human race to survive.
The reason why this is an impermissible choice of reference class is that it is defined
with reference to yourself -- all humans born as late as or later than you were.
Such a customized reference class fails because there is a systematic dependence between
you and the reference class. It would definitely be wrong of you to regard yourself as a
random sample from the population of all humans born on or after your date of birth.
It may be worth illustrating this randomness-proviso with a more mundane example.
Suppose you are doing your laundry in a new washing machine which for all you know may
stop with equal probability any time between the starting point and one hour later, but by
then it must have stopped. You start it and go away to watch telly. After fifteen minutes
you return to make an inspection and you find that it is still running. What is the
probability that it will still be operating after another half hour?
Well, we can think of the stopping time as a uniformly distributed random variable
which has been given an unknown value between 0 and 60 minutes. Checking the machine tells
us that the value wasn't between 0 and 15. We can thus cut away that segment and
renormalize the variable between 15 and 60. So the chance is one third that it is running
at 45 minutes after time zero.
That is how we would normally reason. But now assume that the time of the inspection
was neither chosen at random nor was determined by some other external factor but that it
was instead fixed by randomly selecting a time point from all the time points at which the
machine would be running. For example, if what determined when the machine is to stop is
some kind of hidden timer, then one could have a computer read off that timer and then
select a random number between zero and the preset timer value. Now if you decided to make
the inspection at the time selected by this computer, then the inspection itself would
give you no information, since you were guaranteed that the machine would still be running
at that time; but the clock value when you made your inspection would contain information
that you could use to calculate when the machine were likely to stop. For instance, if the
inspection were made after only two minutes and five seconds, then that would give strong
reason to believe that the machine would have ceased its toil within, say, ten more
minutes.
It would evidently be wrong to reason that the machine was very likely to stop within
the next thirty seconds because "if the machine were to continue to run for more than
thirty seconds then the inspection call would have occurred extraordinarily early in the
interval delta = (2 minutes, machine's stopping time). This would be faulty reasoning
because the time of the inspection call is a random sample from delta-prime = (0,
machine's stopping time), but not a random sample from delta. The faulty interval, or
reference class, was defined by means of a reference to the time the sample was taken. The
lesson is that, as a rule of thumb, one should not define the reference class in the DA by
means of implicit or explicit reference to oneself.
This is, in my opinion, the right response from the advocate of the DA to problems
stemming from an unduly narrowing of the reference class. Leslie, however, takes another
route, which he says was suggested to him by Carter (Leslie [1996], p. 262). He thinks
that defining the reference class as humans-born-as-late-as-you-or-later is fine and that
ordinary inductive knowledge will make the priors so low that no absurd consequences will
follow:
Imagine that you'd been born knowing all about Bayesian calculations and about human
history. The prior probability of the human race ending in the very week you were born
ought presumably to have struck you as extremely tiny. And that's quite enough to allow
us to say the following: that although, if the human race had been going to last for
another century, people born in the week in question would have been exceptionally early
in the class of those-born-either-in-that-week-or-in-the-following-century, this would
have been a poor reason for you to expect the race to end in that week, instead of lasting
for another century. [My emphasis.]
I disagree witn the claim that the prior inductive improbability is enough to allow us
to say this (given that the DA is correct). This insufficiency of the inductive
improbability to compensate for the artificial reference class follows logically from the
fact that the inductive evidence (for the hypothesis that mankind will end in a given time
interval, say within a week from now) is constant no matter how we define the reference
class, whereas the reference class can be defined in arbitrarily many ways, thereby
varying the strength of the resulting probability shift. The inductive evidence could
therefore compensate for at most one strength of the shift, whilst for all other choices
of reference class, a different, incompatible, prediction about our future would result.
It is true that we can always choose the values we substitute for the variables
representing the priors in the Bayesian formula in such a way that we reproduce the
posterior probability resulting from the correct choice of reference class and priors; but
these values which we substitute will then no longer be the prior probabilities but mere ad
hoc numbers chosen because, inserted into Bayes' formula, they happen to give the
output we had decided in advance we wanted to get. Instead of Bayes' formula we could have
used any function onto [0,1], or simply not bothered at all.
I therefore conclude that, contrary to what Leslie and Carter assert, it is essential
that the reference class not be improperly restricted by means of overt or covert
reference to the subject applying the DA.
We have also seen that the reference class must not be too wide: for instance, it must
not include noncognitive beings. Further, we saw that there was an element of choice: we
can device different versions of the DA, depending on what feature of the future we want
to predict; provided, of course, that we don't make the reference class too wide or
confine it in an illegitimate way. These specifications are not sufficient, however, to
completely disambiguate the DA. In particular, we need to know what things, if any, must
be excluded from the reference class except noncognitive beings, and what probability
metric to use over the reference class we choose. We shall address these issues in a later
section.
The Self-Indication Axiom
What I call the self-indication axiom is defined as
follows:
(SIA) The fact that I am an observer gives me some reason to believe that the world
contains many observers.
"Observer" should here be taken to denote those entities which can be
justifiably included in the reference class of the DA. For example, a noncognitive thing
is not an observer, but exactly what types of cognitive things are observers has
not been definitely settled by our discussion so far. "the world contains"
should be understood in the atemporal sense.
The motivation for defining this axiom is that if we accept it then that buys us a very
neat "solution" to the DA problem, i.e. a way of giving all the arguments
advanced by Carter and Leslie their due without changing our minds one bit about the
future of our species and its robotic descendants. The idea is that we could grant that a
shift must be made (a conclusion we seem to have established with the "Amnesia
Chamber"-argument above) while insisting that this shift is counterbalanced by the
greater a priori likelihood of there being many observers. Intuitively, if a world
contains more observers, then there are in some sense more "slots to be born
into", and hence a greater probability that you should find yourself in such a world
rather than in a world that only contains a few observers. Prima facie, the SIA is
admittedly dubious, and perhaps it is no less dubious ultimo facie, but it deserves
serious consideration as it might be the only consistent way of resisting the conclusion
of the DA. We postpone the evaluation to the next section and concentrate here on how it
works to achieve this result.
The easiest way to explain this is to take again the example of God's coin tosses.
Assume it is tossed only once in an otherwise empty universe, creating either ten or one
individual (and neglect the existence of God Himself; it is better to assume that a
mindless machine was responsible for creating the humans). According to the SIA, before
you know anything else than that you were created as a result of that coin toss, you
should believe that the probability of heads is greater than that of tails. On the
simplest version, the chances of heads might be 10:1, for if it did then there would be
ten times more "opportunities for you to exist" than if tails, and since you
know you exist, this should increase the likelihood of the hypothesis which made that more
probable, i.e. (assuming the SIA) the hypothesis that the coin landed heads.
So if we assume the SIA, then we have two effects to consider. First, the SIA says that
finding yourself alive indicates that there are many observers in the world. Second, the
DA says that finding yourself to be in the early group (i.e. finding that you have a rank
that would have existed whether FEW or MANY were true), indicates that there are only few
observers in the world. The neat thing is that, as first noted by Dieks [1992] and shown
by Kopf et al. [1994], these two effects cancel each other out precisely!
Even were we convinced that the SIA is true, we would still have to be careful when we
advocated it or we would risk creating more confusion than we would sort out. For the SIA
would only be to be recommended with the proviso that when we apply it to practical cases,
we must not forget to take the second step in our calculations if the total available
information allows us to do so. Otherwise the probability estimates we come up with will
not reflect the true implications of the data we are analysing. This always true when we
are estimating probabilities, but it is especially pertinent to point it out in this case
because in practice we will always have more information available than goes into the SIA.
Moreover, if we reject an inference of the DA type, as many of us are inclined to do, then
we must also abstain from applying the SIA: we should either apply both considerations or
none. From a pedagogical point of view it could even be argued that it would advisable to
regard the SIA as unsound, for people will tend not to make the DA probability shift in
any case, so one would hardly do them a favour by insisting that they use the SIA, unless
one went to great length to explain the whole situation. There is nothing deep or very
subtle about this. Either you cross the street or you stay on the pavement, and in both
cases you will be safe; but if you stop midway you’ll get run over by a bus.
If the SIA is accepted then the DA is obliterated, without residue. But is the SIA
true? Leslie does not think so, of course, and Dieks did not seriously attempt to give
independent motivation for what I have called the SIA. So how are we to decide?
In general one would expect that most arguments working against the DA would also be
arguments working in favour of the SIA, and vice versa, simply because the SIA is
such a plausible way for the DA to fail, if indeed it does. In the remainder of this
section we will focus on four arguments that are more directly aimed at the SIA: (1) the
argument involving IPC considerations (to be explained in a moment), (2) the argument from
expected utility, (3) the argument from infinity, and (4) the argument from no
coincidence.
1. IPC considerations
One argument, presented in the following paragraph (and which is
subsequently to be shown to be flawed), attempts to show that the 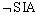 is what I shall call interpersonal congruence violating
(IPC violating). An alleged principle of rationality is IPC violating iff it violates
is what I shall call interpersonal congruence violating
(IPC violating). An alleged principle of rationality is IPC violating iff it violates
(IPC) In any idealised betting context, if a group of persons have exactly the same
priors, equivalent information sets (up to "indexical facts" of the type "I
am Mr. B"), the same preferences, and accept the same canons of rationality, then no
bet is possible between them from which they should all expect to benefit.
The meaning of the IPC condition will be made clearer as we proceed.
One (fallacious) argument that the negation of SIA is
IPC violating
"Consider again the thought experiment with God’s coin
tosses. If we modify the experiment to include one additional person, the owner of a
nearby betting shop, then this wouldn't change anything essential. (We can see this if we
transform the experiment so that instead of one or ten persons being created, either one
billion or ten billion persons are created; the bookie can be made an arbitrarily small
part of the scheme.) But if one refused to accept the SIA then one would have no good
reason to decline a bet on whether God’s coin had landed heads or tails that gave us
a 50:50 + e odds for tails. The bookie, on the other hand,
would have a very good reason to offer everybody such a bet: he would buy a 50% chance of
winning 10 * s for the prize of a 50% risk of losing 1 * s * (1 + e
). Surely he would be irrational not to offer you that bet in this idealised situation.
But then, how could it be rational of you to accept it? For you have exactly the same
information as the bookie, and we can also assume that you accept the same canons of
rationality and make the same estimates of all the prior probabilities.
Both you and the bookie know that God has made his toss of a fair coin and created
either ten or one human as a result. You both know that you, the bet-taker, are alive;
that you were created because of the coin toss. Neither of you has seen how the coin
landed. What other relevant discrepancy between your information sets is there to warrant
the divergence of your probability estimates?
There is none; your sets of relevant information are the same, and therefore your
rational probability estimates must coincide. But since the bookie is obviously rational
to offer you the bet, there must be something wrong with the principle that leads you to
accept it and expect to benefit from it. This principle is the principle that your
existence does not give you any reason whatever to believe that many observers will ever
exist, not even "other things equal" as in this idealised case. Thus we should
reject this principle. If we also reject the implausible principle that your existence
indicates that few observers will ever live (an argument for rejecting that
principle could be construed along the same lines), then we are logically forced to adopt
principle SIA, which is, in effect, no more than the negation of both of these two
rejected principles."
In response to this, the advocate of the DA could choose to sacrifice the IPC and admit
that it may be violated in the contexts where the DA applies. I think this would be pretty
damning for the DA. It would then begin to seem more plausible to assume the SIA, if we
could thereby avoid IPC violation.
There is, however, a definite flaw in the argument above. It was claimed that by
introducing a bookmaker in the God’s coin toss example, we didn’t change
anything essential. But that's not the case. Whereas it is true that by scaling up the
numbers of people that are created as a result of the coin toss we can make the change in
these people’s rational probability estimates due to the introduction of the bookie
arbitrarily small, the same does not hold for the bookie’s rational
probability estimates! The more people that are created as a result of the coin toss
whichever way it landed, the more surprising it should be for the bookie to find himself
being the bookie rather than one of the people in the experiment. One could think that
since the potential gain from offering bets that the coin landed heads are much greater
for the bookie than the potential loss, it would be rational for him to offer bets at a
price at which it would be advantageous for the subjects in the group to accept it (in
conflict with the IPC). This reasoning, however, overlooks the fact that it would be
unlikely in the first place that the bookie would be the bookie if there were many other
roles he could have been in instead. So from observing that he himself is the bookie, he
obtains evidence that the coin probably landed tails. It turns out that this effect
exactly counterbalances the factor defining the quotients of the potential gains to the
potential loss.
Since it is not trivial to see that the compensation is precise, we have to perform a
calculation. We want to show that the fair odds, y, for the bookie are the same as the
fair odds, x, for the subjects in the group. Since everybody have the same information
sets etc., this is a necessary requirement if we are to avoid IPC violation. In order to
prevent ambiguity, we attach the subscript "y" to all the probabilities that are
associated with the bookie, and the subscript "x" to all those associated with
the subjects in the group. We can then write the conditions for fairness of the odds as
 .
.
and

We have already derived  . We
can reduce
. We
can reduce  to known quantities using Bayes’ theorem:
to known quantities using Bayes’ theorem:

If we solve the two formulae representing the fairness conditions, solve them for for x
and y respectively, and then set x = y, we get
 ($)
($)
Thus ($) is the equality that must be satisfied if the IPC condition is not to be
violated. Some algebraic manipulation can take ($) into an equivalent expression that is
more useful if we want to check whether it is satisfied by specific numbers
 ($$)
($$)
where we have introduced the abbreviations



In the special case we discussed above, the parameter values were {R=1, f=1, m=10,
N=1}, and it turns out that they satisfy ($). Numerical calculations indicate that this
holds for all parameter values. Thus 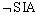 is
not violated in these (quite general) situations. Note that this has as a
consequence, however, that, provided the subjects in the group assign the same priors as
the bookmaker, the condition ($) is always satisfied. This means that the SIA is
not IPC violating either! Thus we find that the IPC requirement cannot be used to arbiter
between SIA and
is
not violated in these (quite general) situations. Note that this has as a
consequence, however, that, provided the subjects in the group assign the same priors as
the bookmaker, the condition ($) is always satisfied. This means that the SIA is
not IPC violating either! Thus we find that the IPC requirement cannot be used to arbiter
between SIA and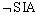 .
.
2. Expected utility
Another argument for the SIA might be derived from the fact that
acceptance of the SIA will maximize a quantity that we can call epistemic utility.
In the simplest case the idea is that when a coin is tossed once and either one or ten
humans are created, and there are no outsiders, then if the SIA is generally adopted as a
principle of rationality, so that the people created will believe that the coin landed
heads, then there would either be ten persons who were right or there would be one person
who was wrong. If, on the other hand, the negation of the SIA were generally adopted, so
that people made their guesses at random, then on average there would be either half a
person who was right or five persons who were right; and that outcome seems inferior to
the outcome if the SIA were generally accepted.



So if the maximizing epistemic utility is what we are trying to do then we should adopt
the SIA. This would then have the consequence that the shift we have to make after finding
that we have a low birth rank would be exactly cancelled by the initial higher probability
that many observers exist; as we saw in a previous section. Thus the DA would fail.
It is, however, far from clear that maximising epistemic utility is our concern here.
If I am trying to decide how likely it is that mankind will go extinct soon, then the
probabilities I am interested in are the probabilities which it would be most rational for
me to accept. How many other persons will be right or wrong seems entirely
irrelevant.
Consider a case where you are being closely monitored by a sexist king who has the
power to instil beliefs in a large portion of the population, though propaganda etc.
Suppose you have good reasons to believe that if the monarch would find that you believe
that his first child will be a son then he will be in a good humour and instil true
beliefs in his people; and that if you believe that his first child will be a daughter
then the opposite will happen. Would this make it overwhelmingly likely that the queen
will give birth to a boy?
It seems that there is a sense of "rationality" according to which it would
be irrational for you to believe that the probability that first child will be a boy is
anything other than about 50% (depending on your earlier experience). In this sense of
rationality it would, analogously, be wrong to regard the greater expected epistemic
utility of the SIA as a reason for its rationality.
Given some more facts about the situation and the likely outcome of your actions, it
may of course be instrumental for you to adopt the belief that there is a 99% chance that
the king's first child will be a son. (Perhaps you have to drink some magical brew to be
able to believe this). If this were so, then there would also be a sense of rationality
according to which it would be rational for you to believe (or to adopt the belief) that
the chance of a son is 99%. This is the sense of rationality according to which an option
(e.g. changing one of your beliefs) is rational only if there is no other option that has
a greater expected utility. However, if we take rationality in this sense, then the
conclusion does not carry over to the DA. For we have not seen any reason to believe that
adopting the SIA would maximize expected utility.
The calculation above indicated that acceptance of the SIA would maximize expected epistemic
utility, in a certain rather contrived sense. But that is something completely
different from expected utility simpliciter. There is no obvious reason to believe
that the world would be more likely to become a better place if the SIA is accepted than
if its negation is. Perhaps it could even be argued that the important thing, if we want
to maximise the chances of making the world a better place, is that as large a fraction
as possible of the people who exist, regardless of how many they are or will have been,
have views that are correct. (Because that determines what democratic decisions are made.)
In that case the argument would rather favour the 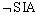 . (This could be true even if people having true beliefs were the sole good.
It would still not follow that it would be irrational in this sense not to accept SIA. For
whereas the SIA would score better than its negation in the context of the DA, there are
many other areas of knowledge that would presumably be best served by whatever principle
it is (SIA or
. (This could be true even if people having true beliefs were the sole good.
It would still not follow that it would be irrational in this sense not to accept SIA. For
whereas the SIA would score better than its negation in the context of the DA, there are
many other areas of knowledge that would presumably be best served by whatever principle
it is (SIA or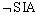 ) that, if adopted, would be
most likely to lead as large a fraction of existing people to be right; the absolute
numbers seem less important. Only if the good equals the number of people who hold correct
views about when mankind will become extinct would an expected utility argument show that
it would be rational to favour the general acceptance of the SIA, in the instrumental
sense of rationality.)
) that, if adopted, would be
most likely to lead as large a fraction of existing people to be right; the absolute
numbers seem less important. Only if the good equals the number of people who hold correct
views about when mankind will become extinct would an expected utility argument show that
it would be rational to favour the general acceptance of the SIA, in the instrumental
sense of rationality.)
The conclusion is that whether we are talking about maximising your immediate
likelihood of being right or about maximising any plausible form of expected utility then
the above argument fails to support the claim for superiority of the SIA to its negation.
3. The problem of infinity
One of Leslie's favourite objections against the SIA is that it
would lead to the conclusion that it is certain that the world contains infinitely
many observers. For so long as our prior probability of the world containing infinitely
many observers is greater than zero then any plausible formalization of the SIA would seem
to imply that the posterior (before the DA is applied) is infinitely probable, i.e.
certain.
One could think that this might not matter, if the application of the DA were then to
restore the status quo. But imagine a situation (the amnesia chamber) where you
happened not to know your birth rank: there you would now have to say that with
probability one the world contains infinitely many individuals, despite the knowledge you
might possess that the observers in the universe were caused by a random process which was
extremely unlikely to generate infinitely many of them. This would clearly be a highly
counterintuitive consequence.
I think infinity problem is very serious for the proponent of the SIA, though as it
stands I don't think it amounts to a conclusive refutation. What are the loopholes? One
could perhaps hope to formalize some variant of the SIA that would somehow discount very
large shifts, or make some kind of renormalization, but I don't see how this could be done
without violating basic Bayesian principles. Alternatively, one might bite the bullet and
accept that had we not known our birth rank then we should indeed assign probability one
to the propositions that the universe contains infinitely many observers. Perhaps some
would try to motivate this move by saying that, although counterintuitive, that wouldn't
matter for practical purposes since we always know our approximate birth rank. This
motivation is wrong though, because we are not looking for a rule of thumb but for a way
to determine whether the DA is correct or not. Yet another escape route would be to say
that infinities cause lots of problems in decision theory and probability theory anyway
(consider Pascal’s wager for example), so it's not particularly blemishing for the
SIA that they cause problems for the SIA too. Another route still would be to argue that
for some deep reason, we should really have expected all along that it would be certain
that the world contains infinitely many observers. For instance, one could follow David
Lewis and believe that all possible worlds exist.
4. No coincidence, no surprise
A further blow is dealt the SIA by the following consideration. A
slightly naïve-sounding but useful way of putting it is in terms of coincidences
(following Derek Parfit [1997] and personal communication). A coincidence is something
that requires two independent things that coincide; one thing makes no coincidence. Now,
if I am in the amnesia chamber and learn that my birth rank is very low then there is a
coincidence: the coincidence between me (the one that is here and now, in the
amnesia chamber) and a certain (very low) birth rank. These two things are
independent, at least as far as I know in the amnesia chamber.
But what are the two independent things in the case of the shift that the SIA
postulates that I should make after "finding myself alive"? One thing is me
(the guy that is here and now). But the other --me being alive -- could hardly be
said to be independent of the first thing. The only reason why me was picked out as
the first thing was that there happened to be a real person (me) who chose to take himself
as a random sample. It is not surprising that a non-existing, merely possible human, was
not picked out as the first thing; -- for there would be nobody to pick him. Thus the
second thing (me being alive), far from being independent of the first thing, was
in fact a necessary prerequisite for the choice of the first thing.
If we wanted to modify this second case so that we would have something where there was
a coincidence, what we would have to do would be to create a big urn with paper slips
containing descriptions of all possible humans or observers. Then we would draw a paper
slip randomly from that urn, and then send somebody out in the world to check if the
possible observer described on that slip is actual. If he or she is, then this would give
us increased reason to believe the world contains many observers. But failing a procedure
such as this, there is no coincidence; and hence no shift should be made; and hence the
SIA is false.
This argument holds some persuasive and explanatory power, at least for me. But
formulated as it is in rather loose terms it cannot be regarded as a conclusive refutation
of the SIA.
A summary of the reasons for and against the SIA
One of the central issues involved in the assessment of the DA is
the self-indication axiom, the SIA. In this section we have discussed four main arguments
that are directly related to the SIA. The first was an argument stemming from
considerations about IPC violation. It was hoped that such considerations would show that
the 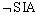 were IPC violating, thereby giving us
strong reason to adopt the SIA and thereby to reject the DA. It was found that neither the
were IPC violating, thereby giving us
strong reason to adopt the SIA and thereby to reject the DA. It was found that neither the
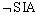 nor the SIA is IPC violating. The second
argument tried to support the SIA by means of calculating "expected epistemic
utilities". This argument was shown to be wrong. The third argument noted that
adoption of the SIA seems to lead to the prediction that with probability one the universe
contains infinitely many observers. This was assessed as a weighty problem with the SIA,
though not one that has (yet) conclusively shown the SIA to be false. The last argument
pointed out that there is a sharp disanalogy between shift postulated by the DA and the
shift resulting from starting to adopt the SIA: the former shift is motivated by the
existence of a significant coincidence, the latter shift lacks such motivation.
nor the SIA is IPC violating. The second
argument tried to support the SIA by means of calculating "expected epistemic
utilities". This argument was shown to be wrong. The third argument noted that
adoption of the SIA seems to lead to the prediction that with probability one the universe
contains infinitely many observers. This was assessed as a weighty problem with the SIA,
though not one that has (yet) conclusively shown the SIA to be false. The last argument
pointed out that there is a sharp disanalogy between shift postulated by the DA and the
shift resulting from starting to adopt the SIA: the former shift is motivated by the
existence of a significant coincidence, the latter shift lacks such motivation.
It is fair to say that the outcome of this evaluation is in favour of the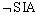 . The only ground for still preferring the SIA
would be if one had overriding reasons to believe that the DA is false and that accepting
the SIA is the only way to maintain this conviction. If that is what one wants to do then
one certainly owes the doomsdayer a couple of good replies to the third and the fourth
argument.
. The only ground for still preferring the SIA
would be if one had overriding reasons to believe that the DA is false and that accepting
the SIA is the only way to maintain this conviction. If that is what one wants to do then
one certainly owes the doomsdayer a couple of good replies to the third and the fourth
argument.
You as a random sample
Let's now make a new stab at the problem of the reference
class.
We have already seen that though your choice of a reference class contains an element
of arbitrariness, it is also restricted by the requirement that non-cognitive things must
be excluded and that it must not make explicit or implicit reference to yourself. The
problem is now to determine what cognitive things can be included.
The question you must ask yourself is this: "What are the probability
distributions from which, according to the rival hypotheses, respectively, you should
regard your birth rank as a random sample?". Given these distributions then you
can straightforwardly apply Bayes' rule to derive the new probabilities of the hypotheses.
To my knowledge, nobody has been able to answer this question convincingly. Let us list
a number of possible answers with some degree of prima facie plausibility:
The individuals to which the distributions assign non-zero probabilities (roughly:
individuals which you could have turned out to have been, had you suffered amnesia and
were subsequently to rediscover your identity) are all:
Individuals who would actually have thought about the DA, given that the hypothesis (on
which they exist) were true.
Individuals who could have understood about the DA, i.e. who are intelligent
enough to understand the argument were it to be explained to them.
Individuals who possess a conception of their own approximate place in human history.
Individuals who have self-awareness.
Individuals who are conscious.
All of these possible maximal reference classes seem to use criteria that involve
matters of degrees. They are therefore in need of further specification.
As a first improvement, we should substitute "episodes" for
"individuals". That way we will take care of the ambiguity of how to weigh
individuals who spend different amounts of time thinking about the DA; who live
differently long lives; who are awake varying amounts of time; etc. For example, according
to (1) then each moment of thinking about the DA, for each individual, counts as an entity
in the reference class over which the probability distribution is non-zero.
This goes some way towards disambiguation, but there are still problematic grey-zones
left. For instance, an episode of thinking about the DA can come in different degrees of
clarity, intensity and focus. Assuming (1), should we say that if there are equally many
deep, clear as muddled, superficial thinkers about the DA (which is certainly not the
case) then one should expect to find oneself as one of the clear thinkers? Or assuming
(5), are highly intense consciousness-moments to be given more weight than torpid ones?
The question about the probability distribution (i.e. which one of (1)-(5) -- or some
variant of these -- to adopt and how to disambiguate the chosen criterion) is an awkward
one for the proponent of the DA, for two reasons.
First, the conclusion of the DA might vary drastically depending on how we choose the
distributions. For example, if we choose (1) then the preferred conclusion might be that
the people of the future will simply not think about the DA anymore. There could be many
explanations of why that might be. This alternative would not be open to us if we chose
any of (2)-(5). Even if we accept the basic soundness of the DA style reasoning, it is
difficult to know what conclusion to draw until we have settled the question about the
reference class and the distribution over it.
Second, pondering over the reference class question, one may come to wonder whether at
the bottom there really is any fact of the matter at all. If there is no fact of the
matter then the DA proponent would have to defend the implausible-seeming position that it
is a fact of the matter that one of (1)-(5) is right, but there is no fact as to which
one. He would have to argue that our notion of rationality hasn't got sufficiently
high resolution to determine which one of (1)-(5) (or some variant) is the right one, only
that the reference class must not include non-cognitive beings, that it must not be
defined in an ad hoc manner with respect to the subject who is the sample, and that
it must satisfy some other rather general criteria.
Conclusion: There are genuine problems remaining about the reference class. They make
it difficult to say exactly what the DA would show, and they also cast some doubt on its
validity.
So what are we to believe?
The DA has so far withstood all attempts at refutation.
The main reason for still doubting it is its extraordinary nature (anthropic reasoning)
and its shocking conclusion. But how could it be consistently disbelieved? We don’t
want to give up the basics of Bayesianism, and if we don’t do that then there seems
to be no way to avoid making a shift. Our discussion about changing the priors showed that
that course of action didn’t look promising on closer inspection. Keeping the priors
and making the shift, we inevitably end up with a DA-like conclusion. Exactly, or even
approximately, what this conclusion is, we cannot tell, because that depends on how we
define the reference class, and no one knows why we should do that one way rather than
another (which raises an additional suspicion about the DA’s validity).
It should be mentioned that Leslie believes that the conclusion of the DA is much
weakened by the indeterminism of the world, made plausible by quantum physics. I decided
not to treat that aspect in this paper.
The most important further illumination that we now need on the DA is in my opinion on
how to find a way to settle the question about the reference class. If the DA is wrong
then in trying to solve the reference class problem we may hope to find out why it
is wrong. If the DA is right then after the reference class problem is solved, we will
have better grounds for believing it, and we would know what the DA really argues for.
Considering the extremely important beliefs (concerning the very survival of humankind)
that are a stake, it should be a priority to try to resolve these perplexities as soon as
possible.
Acknowledgements
I am grateful to Nigel Armstrong, Wei Dai, Jean-Paul Delahaye, Jean Delhotel, J. F.
G. Eastmond, Hal Finney, Mark Gubrud, Robin Hanson, Colin Howson, Thomas Kopf, Kevin Korb,
John Leslie, Jonathan Oliver, Derek Parfit, David Pearce, Sherri Roush, Anders Sandberg
and Damien Sullivan for valuable comments on some of these thoughts.
Back to anthropic-principle.com
NOTES
See also the articles listed in the reference section,
including the papers by Eckhardt, Dieks, Oliver & Korb, Kopf, T.& Krtous, P.&
Page, D. N., T‹ nnsj¯ , T.,
and Delahaye, and Leslie’s responses to some of these, as well as the discussion in Nature
that followed Gott’s article.
See e.g. Howson & Urbach [1993], pp. 403-11, or Leslie [1996], pp.
218-20.
Leslie [1996] covers most of the material previously published in his
journal articles. For his replies to objections, see especially chapters five and six.
Personal communication. See also Leslie [1996], p. 228.
This thought experiment is also used by Leslie [1996], p. 227 ff.
This argument supports that in the present context we can make what Eckhardt
has called the Human Randomness Assumption. Cf. Eckhardt [1997], p. 248.
Leslie [1996], p. 262
It is possible and might be advisable to substitute the following weaker
formulation:
(SIA-) The world is a priori more likely to contain many observers than to
contain few.
This achieves the same effect as the (SIA) while being weaker in that it does not
commit us to a specific view on what a priori grounds it is that make the world likely to
contain many observers.
The calculation is trivial. Let  be
the naive prior for the hypothesis that in total i observers will have existed, and assume
that
be
the naive prior for the hypothesis that in total i observers will have existed, and assume
that  for i greater than some finite N. (This restriction allows us to disregard
the problem of infinities, which we will deal with in a later section.) Then we can
formalize the SIA as saying that
for i greater than some finite N. (This restriction allows us to disregard
the problem of infinities, which we will deal with in a later section.) Then we can
formalize the SIA as saying that

where  is a normalization constant. Let r(x) be the rank of x, and let "I"
denote a random sample from a uniform probability distribution over the set of all
observers. We then have
is a normalization constant. Let r(x) be the rank of x, and let "I"
denote a random sample from a uniform probability distribution over the set of all
observers. We then have

We can assume that  . (If not, then the example simplifies to the trivial case where
the hypothesis is conclusively refuted regardless of whether the SIA is accepted.) Using
Bayes’s formula, we can expand the quotient between two possible hypotheses:
. (If not, then the example simplifies to the trivial case where
the hypothesis is conclusively refuted regardless of whether the SIA is accepted.) Using
Bayes’s formula, we can expand the quotient between two possible hypotheses:

and we see that after we have applied both the SIA and the DA, we are back to
the naive probabilities that we started from.
For Leslie's view on the SIA, see [1996], pp. 224-8.
One could think that talking of episodes instead of individuals could screw
up the way the no-outsider requirement works. Suppose there is just one outsider and
either one or ten million insiders. Then, according to the formula we called GDA, this one
outsider won’t make much of a difference to the rational probability estimates of an
insider, relative to the case where no outsider exists. But the life of this outsider
might typically contain many millions of episodes. So now the number of entities in the
outsider class will be counted in millions. However, this won’t change the
probability estimates, provided that each of the lives of the insiders contains as many
episodes as the life of the outsider. This is easy to see if we examine GDA. The variables
that would change value as a result of substituting "episodes" for
"individuals" occur only in quotients, in such a way that it doesn’t
matter, for instance, into how many episodes we divide one hour of thinking about the DA;
the multipliers cancel out
References
Buch, P. 1994. "Future prospects discussed". Nature,
vol. 368, 10 March, p.108.
Carter, B. 1983. "The anthropic principle and its implications for biological
evolution". Phil. Trans. Roy., Soc., Lond., A310, pp. 347-363.
Delahaye, J-P. (1996) Reserche de mod`eles pour l'argument de
l'Apocalypse de Carter-Leslie. Unpublished manuscript.
Dieks, D. 1992. "Doomsday - Or: the Dangers of Statistics". Phil. Quat.
42 (166) pp. 78-84.
Eckhardt, W. 1997. "A Shooting-Room View of Doomsday". Jour. Phil.,
vol. XCIV, no.5.
Eckhardt, W. 1993. "Probability Theory and the Doomsday Argument". Mind,
102, 407, pp. 483-88
Goodman, S. N. 1994. "Future prospects discussed". Nature, vol. 368,
10 March, p.108.
Gott III, R. J. 1994. "Future prospects discussed". Nature,
vol. 368, 10 March, p.108.
Gott III, J. R. 1993. "Implications of the Copernican principle for our future
prospects". Nature, vol. 363, 27 May, pp. 315-319.
Howson, C. & Urbach, P. 1993. Scientific Reasoning: The Bayesian Approach, 2 ed.
Open Court, Chicago, Illinois.
Leslie, J. 1996. The End of the World: The Ethics and Science of Human Extinction.
Routledge.
Leslie, J. 1993. "Doom and Probabilities". Mind, 102, 407, pp. 489-91
Leslie, J. 1992. "Doomsday Revisited". Phil. Quat. 42 (166) pp. 85-87.
Mackay, A. L. 1994. "Future prospects discussed". Nature, vol. 368, 10
March, p.108.
Moravec, H. 1989. Mind Children. Harvard University Press, Harvard.
Nielsen, H. B. 1989. "Did God have to fine tune the laws of nature to create
light?". Acta Physica Polonica B20, 347-363.
Korb, K. B. & Oliver, J. J. 1998. "A refutation of the Doomsday
Argument". Mind. Forthcoming.
Oliver, J. J. & Korb, K. B. 1997. "A Bayesian analysis of the Doomsday
Argument". Technical Report 97/323, Department of Computer Science, Monash
University.
Kopf, T.& Krtous, P.& Page, D. N. 1994. "Too soon for doom gloom". Physics
preprint gr-gc/9407002, v3 4 Jul.
Parfit, D. 1997. The Sharman Memorial Lectures. UCL, March 1997, London.
T‹ nnsj¯ , T. 1997
"Doom Soon?". Inquiry, 40, 243-52.
Wilson, P. A. 1994. "Carter on Anthropic Principle Predictions". Brit. J
Phil. Sci., 45, 241-253.
. Then we have
.
, we get
.
 .
. (GDA)
(GDA) ($)
($) ($$)
($$)